統計学の基礎知識 - 闘うITエンジニアの覚え書き

目次 †

関連
参考
- 統計Web

平均値 †

数式では μ(ミュー) や

\bar{x}

として表される。

μ = \frac{1}{n} \sum_{i = 1}^{n} x_{1}

import numpy as np

x = np.array([1,2,3,4,5])
print(x.mean())  # 3.0

↑

中央値 †

データを小さい順に並べたとき中央に位置する値。

import numpy as np

x = np.array([1,2,3,4,5])
np.median(x)

結果

3.0

↑

最頻値 †

最も頻繁に出現する値。

import numpy as np
import scipy.stats as stats

x = np.array([1,2,3,1,2,3,5,6,3,5,6,7,4,1,3,4])
stats.mode(x, axis=-1).mode[0]

結果

↑

四分位範囲（IQR） †

散らばりの程度を表す尺度の一つ。

四分位範囲(IQR) = 75パーセンタイル(第三四分位数) - 25パーセンタイル(第一四分位数)

data = np.array([2,69,67,75,84,92,80,77,65,78,84,95,71])

# 四分位点を求める
q25, q75 = np.percentile(data, [25 ,75])

# 四分位範囲
iqr = q75 - q25

print(q25, q75 )
print(iqr)

↑

外れ値について †

外れ値の定義は扱われるデータによって変わるが、一般的には、値 < (Q1 - 1.5 * IQR) または値 > (Q3 + 1.5 * IQR) を外れ値として扱う。

例1) 上記のデータから外れ値を除外する例

print(data[(data >= q25 - 1.5 * iqr) & (data <= q75 + 1.5 * iqr)])

結果

[69 67 75 84 92 80 77 65 78 84 95 71]   # 2 が除外されている

例2) 平均 ±Nσ の範囲外を外れ値として扱う場合
※ 平均 ± 標準偏差 * N

# 平均 ±2σ を外れ値として扱う場合
N = 2
s_plus = data.mean() + (N * data.std())
s_minus = data.mean() - (N * data.std())

print(data[(data >= s_minus) & (data <= s_plus)])

結果

[69 67 75 84 92 80 77 65 78 84 95 71]   # 2 が除外されている

↑

分散 †

データのばらつきを表す値。( variance )

1. 各データと平均値の差を求める
2. 1で求めた値を2乗する
3. 2で求めた値をすべて足す
4. 3で求めた値をデータ数で割る

→

s^{2} =

\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}

例)

import numpy as np

x = [1,2,3,4,5]
np.sum((x - np.mean(x)) ** 2) / len(x)   # 2.0

↑

正規分布 †

平均を μ, 分散を

σ^{2}

> 0 とする（1次元）正規分布は、以下の式で表される。

f(x) = \frac{1}{\sqrt{2π}} exp (- \frac{(x - μ) 2}{2 σ^{2}})

↑

標準正規分布 †

平均が0、分散が1の正規分布のこと。

f(x) = \frac{1}{\sqrt{2π}} exp (- \frac{x^{2}}{2})

↑

標準偏差 †

標準偏差を求めるには、分散の平方根(ルート)をとる。

σ = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}

import numpy as np

x = [1,2,3,4,5]

np.std(x)
# 1.4142135623730951

np.sqrt(np.sum((x - np.mean(x)) ** 2) / len(x))
# 1.4142135623730951

↑

不偏分散と標本標準偏差 †

不偏分散の平方根をとる事で標本標準偏差を求める事ができる。
※不偏分散は、標本分散から母分散を推測するための分散で全標本数-1で割る。

標本標準偏差 = \sqrt{\frac{1}{(n - 1)} \sum_{i = 1}^{n} {(x - \bar{x})}^{2}}

data = np.array([...])
np.sqrt(np.sum((data - m) ** 2) / (len(data) - 1))

↑

偏差値の求め方 †

偏差値は、元のデータを平均が50、標準偏差が10となるように変換した値。

偏差値 = \frac{x - \bar{x}}{s} * 10 + 50

※ s: 標準偏差

score = np.array([82, 95, 74, 65, 77, 88])

# 標準偏差
s = np.sqrt(((score - score.mean()) ** 2).sum() / (len(score)))

# 偏差値
print((score - score.mean()) / s * 10 + 50)

結果

[51.89289775 65.31526361 43.6329803  34.34057317 46.73044934 58.08783584]

↑

Z得点（z値、z-score、z-value） †

平均が0、標準偏差（SD）が1になるように変換した得点。
※平均から標準偏差何個ぶん離れているか。
※ z = (データ - 平均) / 標準偏差

z = \frac{x - μ}{σ}

↑

相関係数 †

相関係数は相関関係の強弱を数値化したもの。
※相関係数は -1 <= r <= 1 の値を持ち、1 (または -1) に近いほど相関関係が強い。

r = \frac{x と y の共分散}{xの標準偏差 ・ yの標準偏差} = \frac{S_{xy}}{S_{x} S_{y}} = \frac{\frac{1}{n} \sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}

x = np.array([82, 95, 74, 65, 77, 88])
y = np.array([2, 3, 1.5, 0.5, 1, 1.5])

n = x.size
x_mean = x.mean()
y_mean = y.mean()
x_std = x.std()
y_std = y.std()

# x と y の共分散を求める
cov = np.sum([(x - x_mean) * (y - y_mean)]) / n
# cov = np.cov(x, y, ddof=0)[0][1]   # 共分散は np.cov でも求める事ができる

# 相関係数を求める
r = cov / (x_std * y_std)

print(r)
print(np.corrcoef(x, y))  # 相関係数は np.corrcoef でも求める事ができる

結果

0.8737254372984308
[[1.         0.87372544]
 [0.87372544 1.        ]]

↑

非線形の相関 †

上記のピアソンの相関係数で数値化できるデータは線形の相関に限られる。
例えば、以下のように明らかに関係性があるデータでもピアソンの相関係数では正しい相関度を表す事ができない。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 200)
y = x**2

plt.plot(x, y, marker="o")
plt.show()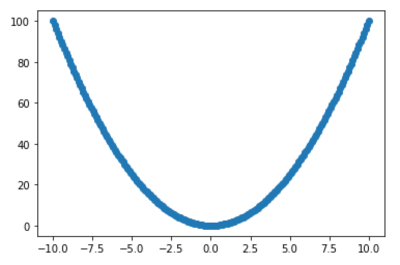

ピアソンの相関係数

print('{:0.20f}'.format(np.corrcoef(x, y)[0,1]))

結果

0.00000000000000019357

MIC( Maximal information coefficient )を使用すると、このような非線形の相関も表す事ができる。

from minepy import MINE

mine = MINE()
mine.compute_score(x, y)
print('{:0.20f}'.format(mine.mic()))

結果

0.99999999999999888978

↑

標準化係数 †

(データ - 平均) / 標準偏差
※標準偏差何個分離れているか (平均を1とする)
※正規分布の場合、±1 以内は全体の 68% に含まれる。( 正規分布の「68-95-99.7ルール」 )

↑

帰無仮説 †

統計的仮説検定の際にとりあえず立てる仮説の事。

H^{0}

として表される。

↑

P値 †

帰無仮説の下でデータから計算された統計量よりも極端な(仮説に反する)統計量が観測される確率をP値という
一般的にP値が5％または1％以下の場合に帰無仮説を偽として棄却し、対立仮説を採択する。

↑

有意水準 †

どの程度の正確さをもって帰無仮説

H^{0}

を棄却するかを表す定数。
有意水準αの仮説検定は、p < α の時に

H^{0}

を棄却する

↑

検出力 †

統計的仮説検定で、帰無仮説が偽であるときに検定が帰無仮説を棄却する確率の事。

↑

t検定 †

TODO:

↑

加重平均 †

異なる母数を持つ複数の平均の平均を求める

↑

平均 ±Nσ †

平均 ± 標準偏差 * N (範囲外は外れ値として扱う。等)

↑

効果量 †

TODO:

↑

その他 †

↑

正規分布の「68-95-99.7ルール」 †

TODO:

↑

標準正規分布表(Zテーブル)を使用した分布率の算出 †

TODO:

最新の20件

統計学の基礎知識 - 闘うITエンジニアの覚え書き

テスト

ビルド

開発メモ

プロジェクト管理

ｻｰﾊﾞ/ｼｽﾃﾑ管理

サーバ/DB関連

その他

目次 †

平均値 †

中央値 †

最頻値 †

四分位範囲（IQR） †

外れ値について †

分散 †

正規分布 †

標準正規分布 †

標準偏差 †

不偏分散と標本標準偏差 †

偏差値の求め方 †

Z得点（z値、z-score、z-value） †

相関係数 †

非線形の相関 †

標準化係数 †

帰無仮説 †

P値 †

有意水準 †

検出力 †

t検定 †

加重平均 †

平均 ±Nσ †

効果量 †

その他 †

正規分布の「68-95-99.7ルール」 †

標準正規分布表(Zテーブル)を使用した分布率の算出 †